CHAPTER O2 PART B POLYNOMIALS
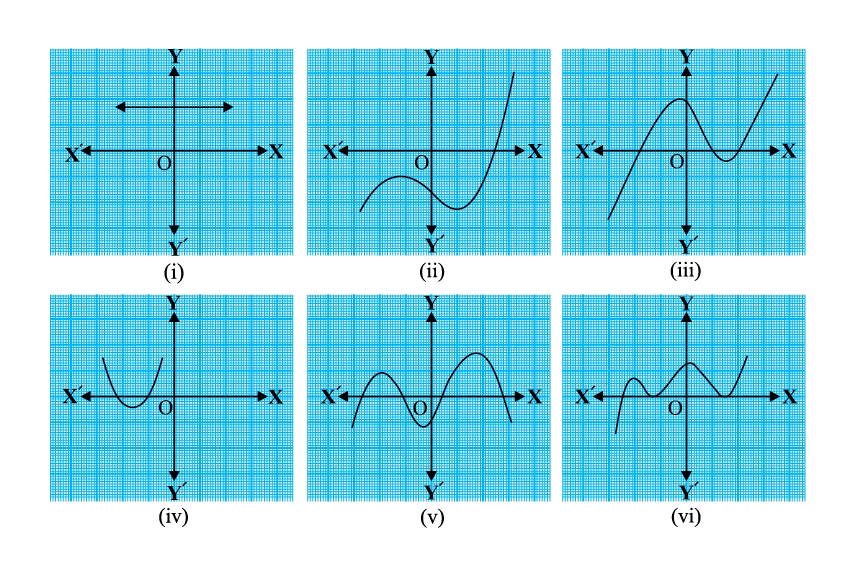
In the Figure given below, find the number of zeroes in each case.
How to Calculate Zeroes, when the Graph of a Polynomial has been given ?
The Zeroes of a Polynomial indicates the values of 'x' at which the value of polynomial p(x) becomes zero. Hence In a Grapgh plotted for the Polynomial, the points at which the value of Polynomials becomes zero, or the points at which graph either interset or touch the 'x' axis gives the zeroes of that Polynomial.
If a Polynomial does not intersect or touch the 'x' axis at any point, it indicates that the Polynomial does not have any zeroes.
Figure 1. As the given graph of the Polynomial does not intersect 'x' axis at any point, it indicates that the Polynomial does not have any zeroes.
Figure 2.
The Polynomials Grapgh intersect the 'x' axis at exactly one point, so Polynomial has one zeroes.
Figure 3
The Polynomial interset the 'x' axis at three points. It indicates that the Polynomial have three zeroes.
Figure 4
The Polynomial Graph intersect the 'x' axis at two exact points. So the Polynomial have two zeroes.
Figure 5
The Polynomial Graph intersect the 'x' axis at 04 exact points, so the Polynomial have four zeroes.
Figure 06
The Polynomial Grapgh touches the 'x' axis at two points and intersect the 'x' axis at one point. It implies that Polynomial have zeroes out of which one is unique and other two are similar.
Thank you Very Much
Please like share and comment.
Feel free to give your suggestions and feedback in the comment section below.
To read More Such Posts related to Class 10 Click on the Links Given Below :-