Showing posts with label Class 10 Math. Show all posts
Showing posts with label Class 10 Math. Show all posts
0

Problems dated Nov 05 2021

posted on , by UDBHAV

Problems Dated Nov 05 2021. Problem No 09 First Number = x Second Number =y Case 1 (x+2)/(y+2) = 1/2Case 2 (x-4)/(y-4) = 5/11From 1 2x - y = -2 ...... 3 from 2 11x - 5y = 24 .... 4 Multiplying Eqn 1 by 5 10 x - 5y = -10   .......5Eqn 4 -Eqn 5 11x - 5y -10 x + 5y = 24 + 10 x = 34 From Eqn 1 2 (34) - y = ...

Read More
0

Linear Eqn in Two Variables.

posted on , by UDBHAV

 Exercise 3E R S Agarwal Problem No 01 Chair = x Tables = y 5 x + 4 y = 5600 ..... 1 4 x + 3 y = 4340 ....... 2 1 * 4  &  2 * 5 20x + 16 y = 22400.......... a 20x + 15y = 21700............b a-b y = 7005x + 2800 = 5600 5x = 2800 x = 560 Ans Problem No 02 To read More Such Posts related ...

Read More
0

Maths Problems dated 03 Nov 2021

posted on , by UDBHAV

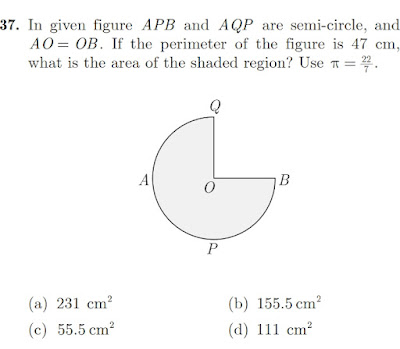
 MISCMaths Problems dated 03 Nov 2021Problem No 01In the given figure APB and AQB are two semi circle. (Given) Perimeter of the given shape will be equal to = Circumference of half semi circle (APB) + Circumference of quarter semicircle AQO + QO RADIUS + OB RADIUS = ( PI * R ) + (0.5 * PI * R) + R + R But this perimeter is given equal to the 47 cm.Hence, ( ...

Read More
0

Chapter 02 Polynomials

posted on , by UDBHAV

 Chapter 02 Polynomials Problem No 01 :- Find the Zeros of the Polynomials and verify the relationship between the zeros and coefficients :-x2 + 7x + 12To find the zeros of polynomial, It should be equated to zero firstHence,x2 + 7x + 12 = 0Or, x2 + 4x + 3x + 12 = 0Or, x (x + 4)+ 3 (x + 4 ) = 0Or, (x + 3) * (x + 4 ) = 0It implies that x = - 3 & -4 Ans ............................................... (1)Comparing the Given Eqn with Stnd Eqn i.e. ax2 + bx + c = 0We Get, a=1 , b = 7 & ...

Read More
0

CLASS 10 MATHEMATICS

posted on , by UDBHAV

 CLASS 10 MATHEMATICSWelcome All, In this Section,  a collection of problems have been presented from various Books of CBSE Mathematics Class 10. Problems can be seen by clicking on the list of chapters given below :- Real NumbersPolynomialsLinear Equation in Two VariablesTrianglesTrigonometric Ratios. T-Ratios of some Particular Angles. Trigonometric Ratios of Complementary Angles. Trigonometric Identities. Mean, Median, Mode of Grouped Data, Cumulative ...

Read More
0

Class 10 Area

posted on , by UDBHAV

Class 10 Area Answer:- As per the DiagramEC = BC (Radius in Sector BGEC) Hence EC = 7 Cm. DE = 4 cm Given DC = DC + EC = 4 CM + 7 CM = 11 cm Area of trapezium ABCD = (1/2) *( Sum Of ||el sides) * (Height)= (1/2) * (AB+DC) *(BF) =(1/2) * (7 cm + 11 cm ) * (3.5 cm ) = 0.5 * 18 cm * 3.5 cm = 9 cm * 3.5 cm = 31.50 cm2 Area ...

Read More